1、标准差是用来衡量一组数自身的离散程度,而均方根误差是用来衡量观测值同真值之间的偏差,它们的研究对象和研究目的不同,但是计算过程类似RMSE与MAE对比RMSE相当于L2范数,MAE相当于L1范数次数越高,计算结果就越与较大的值有关,而忽略较小的值,所以这就是为什么RMSE针对异常值更敏感的原因msermse区别;在统计学和机器学习的殿堂里,误差指标如同明灯,照亮了模型性能的细微差别首先,我们遇见的是SSE残差平方和,它是模型与实际值之间差异的总和,越接近零,模型的拟合度越高紧接着,MSE均方误差和它的兄弟RMSE均方根误差登场MSE是误差平方的平均值,而RMSE则消除了量纲影响,让我们能msermse区别;回归问题则常用均方误差MSE均方根误差RMSE或平均绝对误差MAE等来评估预测值与真实值之间的偏差4 评估指标 分类问题的评估指标包括准确率精确率召回率F1分数等,用于衡量模型对不同类别的预测性能 回归问题的评估指标包括均方误差均方根误差平均绝对误差等,用于量化。
2、均方误差衡量精度的基石MSE是评价数据预测准确性的核心工具,它衡量的是平均预测误差的平方简单来说,它告诉我们模型预测值与实际值之间差异的平方平均值,直观地反映了数据变化的平均水平从平方到平方根RMSE的出现RMSE是MSE的平方根,是对MSE的一种简化,它提供了更为直观的误差尺度当我们谈论msermse区别;实例1数据点真实值10, 15, 20, 25, 30,预测值102, 151, 198, 252, 301,计算得到RMSE和MAE均为016,两者选择无明显区别实例2数据点真实值10, 15, 20, 25, 30,预测值12, 14, 18, 26, 28,RMSE为158,MAE为16,MAE略大,未存在大误差值影响;探索模型精度判定系数MAPERMSE与MAE的深入解析在评估模型的精确性和预测能力时,我们通常依赖几个关键指标,它们分别是判定系数R2均绝对误差MAE均方误差RMSE和平均绝对百分比误差MAPE每个指标都有其独特的侧重点,理解它们的特性至关重要判定系数R2lt,被誉为模型拟合。
3、在数据分析和测量世界中,误差和精度的度量标准至关重要首先,我们来逐一揭开这些术语的神秘面纱1 均方误差与均方根误差的桥梁 均方误差MSE,如同其名,是数据与真实值间偏差的平方和的平均,它的开方就是我们熟悉的均方根误差RMSE尽管名称上与标准差有所差异,RMSE实际上在形式上更接近;作用衡量预测值与真实值之间差异的绝对值的平均值,对极端值和离群值的反应不如RMSE强烈特点易于计算和理解,能够反映出预测误差的平均水平总结在评估模型性能时,需要根据具体的应用场景和数据特性选择合适的指标R2适用于初步判断模型的拟合程度,而MAPERMSE和MAE则更适用于详细评估预测误差;2 MSE均方差方差MSE是预测数据和原始数据对应点误差的平方和的均值与SSE相似,MSE衡量了模型的预测误差3 RMSE均方根标准差RMSE是MSE的平方根,避免了量纲问题它衡量了模型预测值与实际值之间的差距4 MAE平均绝对误差MAE是绝对误差的平均值与RMSE相比,MAE更直观;相对均方误差RMSE和均方误差MSE都是衡量预测值与实际值之间差异的指标,但它们之间存在一些关键区别1量纲均方误差MSE的单位是原始数据的平方,而相对均方误差RMSE的单位是原始数据因此,RMSE具有更直观的解释性,因为它表示的是预测值与实际值之间的绝对差异2敏感性由于RMSE的。
4、均方差与均方误差的区分 均方差,或称均方差,与均方误差MSE有着微妙的区别MSE是每个数据点与真实值之差的平方和的平均,其计算结果通常用于评估模型预测的精度,而标准差则更多地关注数据与平均值的偏离均方根误差RMSE,MSE的平方根,与标准差形式相似,但侧重点在于误差的大小而非偏离程度;随机森林在处理分类和回归任务时存在几个关键差异首先,对于分类问题,随机森林采用分类决策树,并通过多数投票原则来确定最终类别而对于回归问题,它使用回归决策树来预测连续数值分类问题的性能评价通常基于分类准确率,而回归问题则常用均方误差MSE或均方根误差RMSE来评估其次,随机森林在;均方根误差,它是观测值与真值偏差的平方和观测次数n比值的平方根,在实际测量中,观测次数n总是有限的,真值只能用最可信赖最佳值来代替是方差的算数平方根,是用来衡量一组数自身的离散程度,能更好地反映预测值误差的实际情况相关信息RMS 均方根误差值是干涉图中所有数据点高度的标准偏差;当数据点误差均在较小范围内时,RMSE和MAE的值可能相近,此时选择任意标准皆可当存在较大误差值时,RMSE值会显著增大,而MAE则相对较小若关注大误差值的影响,应选择RMSE若希望平衡考虑所有误差值,无论大小,则选择MAE数值大小比较在没有具体数据点的情况下,无法直接判断RMSE和MAE谁更大。
5、在回归分析中,常用MSE均方误差RMSE均方根误差和MAE平均绝对误差来评估模型性能MSE通过计算预测值与实际值之间的平方差来衡量误差,RMSE是MSE的平方根,使误差单位与原数据一致,MAE通过计算预测值与实际值之间绝对差的平均值来衡量误差在Python的sklearn库中,使用mean_squared_error。
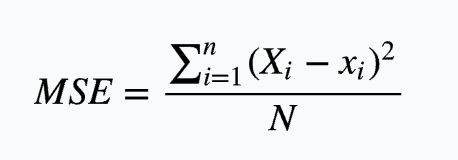
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。
发表评论